6 Inorganic Nitrogen

6.1 Contributors

Daniel Paraska, Louise Bruce, Peisheng Huang, and Matthew R. Hipsey

6.2 Overview

Nitrogen is fundamental to shaping water quality in aquatic ecosystems. Nitrogen is of particular interest in that exists in many redox states and there are a myriad of organic and inorganic reactions that make up the nitrogen biogeochemical system. NO₃^- and NH₄⁺ are the primary inorganic nutrients that are taken up by aquatic plants (phytoplankton, macroalgae and macrophytes) to build biomass as organic nitrogen. As nitrogen is a core building block of an aquatic ecosystem, aed_nitrogen (\(\mathrm{NIT}\)) is designed as a low-level module for managing the inorganic nitrogen pools, and is able to be linked to by higher order modules associated with primary production, organic matter breakdown, and other ecosystem processes.

The general nitrogen redox processes specifically resolved in this module are NH₄⁺ oxidation to NO₃^- by O₂, and NO₃^- reduction to N₂ with organic matter. Advanced options are available, in which the end result is generation of the nitrogen species N₂O. Producing N₂O uses more variables and reaction pathways and is not necessary for most nutrient cycling studies. The module also supports processes associated with the dissolved sediment flux and atmospheric deposition.

Importantly, nitrogen species react with organic matter. The description of organic matter involvement in nitrogen reactions and interactions can be found in Section (OGM). The uptake and use of these variables by phytoplankton and macroalgae are described in Section (PHY) and (MAG).

When configuring the \(\mathrm{NIT}\) module, users must first identify the level of complexity they wish to adopt in their nitrogen module configuration. Whilst the module is highly configurable, users generally adopt the default model, and if N2O or more granuallr resolution of nitrogen redox interactions are required then they can choose these more advanced options via the switch simN2O.

6.3 Model Description - Default Model

6.3.1 Process Descriptions

In the default nitrogen module configuration, the variables NO₃ and NH₄ are included as state variables and able to be modified by nitrification, denitrification, sediment release and atmospheric deposition; to use this basic functionality, ensure the parameter simN2O is set to 0. The main balance equations for these two simulated variables are summarised as:

\[\begin{eqnarray} \frac{D}{Dt}NO_3 = \color{darkgray}{ \mathbb{M} + \mathcal{S} } \quad &+& \overbrace{f_{nitrf}^{NH_4} - f_{denit}^{NO_3} + \check{f}_{atmdep}^{NO_3}+\hat{f}_{sed}^{NO_3}}^\text{aed_nitrogen} \\ \tag{6.1} &-& \color{brown}{ f_{nup}^{PHY} - f_{nup}^{MAG} } \\ \nonumber \end{eqnarray}\] \[\begin{eqnarray} \frac{D}{Dt}NH_4 = \color{darkgray}{ \mathbb{M} + \mathcal{S} } \quad &-& \overbrace{ f_{nitrf}^{NH_4} + \check{f}_{atmdep}^{NH_4}+\hat{f}_{sed}^{NH_4}}^\text{aed_nitrogen} \\ \tag{6.2} &+& \color{brown}{ f_{min}^{DON} - f_{nup}^{PHY} - f_{nup}^{MAG} } \\ \nonumber \end{eqnarray}\]

where \(\mathbb{M}\) and \(\mathcal{S}\) refer to water mixing and boundary source terms, respectively, and the coloured \(\color{brown}{f}\) terms reflect the optionally configurable contributions from other modules; these include the mineralisation of \(DON\) and \(N\) cycling terms associated with photosynthesis and respiration by various biotic groups.

If users wish to include NO₂ or N₂O as state variables in a simulation, then refer to Section X.4

6.3.1.1 Nitrification and denitrification reactions

In an environment of high O₂, NH₄⁺ is oxidized by oxygen to NO₃^- via nitrification. In an environment of low O₂, NO₃^- is reduced to N₂ via the process denitrification. O₂ limitation on the rate of the reaction is not included in the default setup, but can be chosen by the user, as described in the section below.

6.3.1.2 Nitrification

The rate of nitrification is assumed to vary primarily due to temperature, and also due to variation in O₂ and pH, according to:

\[\begin{equation} f_{nitrf}^{NH_4} =R_{nitrf} \; \theta_{nitrif}^{T-20} \; {\underbrace{\Phi_{O2}^{nitrf}\left[O_2\right] \Phi_{pH}^{nitrf}\left[pH\right]}_{\text{Optional limitations}}} \; NH_4 \tag{6.3} \end{equation}\]

where \(\theta_{nitrif}\) is a Arrhenius temperature parameter specific to nitrification, and \(T\) is the temperature produced by the host model. O₂ limitation on this rate will not be included in the setup unless a link to the oxygen module is made, as described in the section below.

Oxygen limitation on nitrification: An extra option is to allow low O₂ concentration to limit the nitrification rate, \(\Phi_{O_{2}}^{nitrf}\left[O_2\right]\). If the aed_oxygen module is linked to the nitrogen module, then this setting will switch on automatically. The limitation effect is calculated according to:

\[\begin{equation} \Phi_{O_{2}}^{nitrf}\left[O_2\right]=\frac{O_2}{O_2+K_{nitrif}} \tag{6.4} \end{equation}\]

where \(K_{nitrif}\) is a half saturation constant concentration of oxygen. The purpose of this factor is to reduce the rate of nitrification as oxygen moves below a critical concentration.

pH limitation on nitrification: The rate of nitrification can be decreased at very high and low pH values, if pH is being simulated (see Carbon and Geochemistry). To use this function, the parameter simNitrfpH is set to .TRUE.. Around neutral pH, between the upper and lower optimum parameters, the reaction proceeds at the normal rate. Below a lower tolerance, and above an upper tolerance, the reaction is stopped entirely. Between the optimum and tolerance values, the rate is limited, in proportion to pH.

Light limitation on nitrification: This process is not currently included and is an open area for contributions.

6.3.1.3 Denitrification

Denitrification is a heterotrophic process occurring in low oxygen environments such as anoxic bottom waters and sediments. In addition to oxygen, the rate of denitrification depends on temperature and nitrate availability. It is calculated according to:

\[\begin{equation} f_{denit}^{NO_3} = R_{denit}\; \theta_{denit}^{T-20}\; \frac{NO_3}{NO_3+K_{NO3}} \; \Phi_{O2}^{denit}\left[O_2\right] NO_3 \tag{6.5} \end{equation}\]

where \(R_{denit}\) is the kinetic rate constant for denitrification and \(\theta_{denit}\) is a temperature parameter specific to denitrification. The Monod term in Equation (6.5) slows the rate at low NO₃^- concentrations, and allows it to proceed at the maximum rate R_denit at high NO₃^- concentrations. The parameter KNO3 is the half-saturation parameter for limiting the reaction rate and is set by the user to slow the rate at low NO₃^- concentrations. This parameter should not be confused with the O₂ limitation factor K_denit, mentioned below; O₂ limitation on the rate of the reaction is not included in the default setup, but can be chosen by the user, as described in the section below.

Oxygen mediation of denitrification: For denitrification, oxygen slows the reaction through inclusion of an inhibition function as:

\[\begin{equation} \Phi_{O2}^{denit}\left[O_2\right]= \left\{\begin{array}{ll} \frac{K_{denit}}{O_{2}+K_{denit}},\ \ \ \ \ \ \ \Theta^{denit}_{oxylim} = 1\\ e^{(-O_{2}/K_{denit})},\ \ \ \Theta^{denit}_{oxylim} = 2\\ \end{array} \right. \tag{6.6} \end{equation}\]

Such that the denitrification rate is inhibited by high O₂ concentrations, using the parameter K_denit. This parameter is an O₂ concentration, and should not be confused with the parameter KNO3 which is a NO₃^- concentration. To use the process shown in Equation (6.6), the switch oxy_lim, \(\Theta_{oxylim}^{denit}\), set to the number 1.

Alternatively, the rate of denitrification can be set to decreases exponentially at high O₂ concentrations, also using the parameter Kdenit. This is the same parameter as for the inhibition function described above, but applied differently.

6.3.1.4 Atmospheric deposition

Nitrogen can be added to the surface cells of an aquatic system through two kinds of atmospheric deposition: wet and dry. These functions can be turned on by setting the parameters simDryDeposition and simWetDeposition to .TRUE..

\[\begin{equation} f_{atmdep}^{NOx}=\left[{\underbrace{F_{atm}^{DIN}}_{\text{Dry flux}}}+{\underbrace{R_n\left[t\right] {DIN}_{atm}}_{\text{Wet flux}}}\right] \frac{{k}_{DINdepNO_x}}{\Delta z_{surf}} \tag{6.7} \end{equation}\] \[\begin{equation} f_{atmdep}^{NH_4}=\left[{\underbrace{F_{atm}^{DIN}}_{\text{Dry flux}}} + {\underbrace{R_n\left[t\right] {DIN}_{atm}}_{\text{Wet flux}}}\right]\frac{\left({1-k}_{DINdepNO_x}\right)}{\Delta z_{surf}} \tag{6.8} \end{equation}\]

where \(\Delta z_{surf}\) is the surface layer thickness. Wet deposition adds nitrogen as a result of rain, \(R_n\) (m/day), which is a variable or a boundary condition provided as an environment variable from the host model. The deposition from rain is proportional to the atmospheric nitrogen concentration atm_din_conc. As with dry deposition, the proportion that is assigned to NO_x and NH₄⁺ is given by the same parameter f_dindep_nox.

6.3.1.5 Sediment flux

NO₃^- and NH₄⁺ can flux into the water column from the sediment, using the parameters \(F_{sed}^{nit}\) and \(F_{sed}^{amm}\), which set the maximum flux rate. The maximum flux rate is limited by temperature, using the parameters theta_sed_nit and theta_sed_amm, according to

\[\begin{equation} f_{sed}^{NOx}=F_{sed}^{nit} \theta_{sednit}^{T-20}\Phi_{O2}^{nit}\left[O_2\right] \tag{6.9} \end{equation}\] \[\begin{equation} f_{sed}^{NH4}=F_{sed}^{amm} \theta_{sedamm}^{T-20}\Phi_{O2}^{amm}\left[O_2\right] \tag{6.10} \end{equation}\]

This assumes that there is a higher flux at higher temperatures; set \(\theta_{sed}=1.0\) to remove any temperature dependance.

Oxygen mediation of the sediment nitrogen fluxes: As with the nitrification reaction, the sediment flux can be changed by bottom water O₂ concentration. If the aed2_oxygen module is correctly linked to the nitrogen module then this setting will switch on automatically. At low O₂ concentrations, the amount of NO₃^- fluxing out of the sediment is decreased and at high O₂ concentrations, it is set close to the F_sed_nit, as shown in Equation (6.11). This is a convenient simplification that can be tuned within this module, rather than a more complicated full set of biogeochemical reactions. The parameter K_sed_nit can be used to tune the NO₃^- flux dependence on bottom water O₂. A similar function can be used to tune the NH₄⁺ flux using the parameter K_sed_amm, as shown in Equation 13. At high O₂ concentrations, NH₄⁺ flux decreases, and at low O₂ concentrations, the flux is close to the parameter F_{sed}^{amm}.

\[\begin{equation} \Phi_{O2}^{nit}\left[O_2\right]=\frac{O_2}{K_{sednit}+O_2} \tag{6.11} \end{equation}\] \[\begin{equation} \Phi_{O2}^{amm}\left[O_2\right]=\frac{K_{sedamm}}{K_{sedamm}+O_2} \tag{6.12} \end{equation}\]

Advanced options: The approach described here is the most simple and default method for capturing DIN fluxes from the sediment, and is sometimes referred to the static model. This approach can be extended to allow for spatial variability in \(F_{sed}^{nit}\) and \(F_{sed}^{amm}\), by engaging the link to the aed_sedflux module, where the host models support multiple benthic cells or zones. In this case, users input spatially discrete values of \(F_{sed}^{nit}\) and \(F_{sed}^{amm}\).

Where dynamic rates of DIN species are required to flux to/from the sediment (e.g. in response to episodic loading of organic material to the sediment, or for assessment of long-term changes in N loading), then the above expressions (Eq (6.9)-(6.12)) are replaced instead with dynamically calculated variables in aed_seddiagenesis, via a link created with the aed_sedflux module.

6.3.2 Variable Summary

The default variables created by this module, and the optionally required linked variables needed for full functionality of this module are summarised in Table X.

6.3.3 Parameter Summary

The default parameters and settings used by this module are summarised in Table @ref(tab:nitrogen_tab1).

Parameter name	Description	Unit	Parameter type	Default	Typical range
Nitrification/Denitrification
R_nitrif	Kinetic rate constant for nitrification	day-1	real	0.01	0.001-0.2
theta_nitrif	Temperature dependence of nitrification		real	1	1.05-1.12
R_denit	Kinetic rate constant for denitrification	day-1	real	0.01
theta_denit	Temperature dependence of denitrification	Unitless	real	1
KNO3	Half saturation constant for NO3- limitation on denitrification	mmol m-3	real	5
Kdenit	O2 inhibition of denitirification or exponential reduction	mmol m-3	real	150
oxy_lim			Integer	1	1 or 2
NITpHTolMin	Minimum tolerance	pH unit	real	5.5
NITpHOptMin	Minimum optimum	pH unit	real	7.1
NITpHOptMax	Maximum optimum	pH unit	real	7.9
NITpHTolMax	Maximum tolerance	pH unit	real	9
Atmospheric Deposition
simDryDeposition	Switch to turn on atmospheric deposition		LOGICAL	TRUE
simWetDeposition	Switch to turn on rain deposition		LOGICAL	TRUE
atm_din_dd	Atmospheric DIN deposition rate	mmol m-2 d-1	real	0
atm_din_conc	Atmospheric DIN composition	mmol m-3	real	0
f_dindep_nox	Fraction of DIN that is NOx		real	0.5
Sediment Flux
Fsed_nit	Sediment NO3- flux
Fsed_amm	Sediment NH4+ flux
Ksed_nit	Sediment NO3- flux	mmol m-2 d-1	real	30
Ksed_amm	Sediment NH4+ flux	mmol m-2 d-1	real	30
theta_sed_nit	Temperature dependence on sediment NO3- flux		real	1
theta_sed_amm	Temperature dependence on sediment NH4+ flux		real	1

6.3.4 Optional Module Links

Other nitrogen sources/sinks are indicated in Eq (6.1)-(6.2). These include:

• Ammonium release during bacterial mineralisation of DON in the organic matter module - aed_organic_matter;
• Nitrate consumption during denitrification of DON in the organic matter module - done in aed_organic_matter if simDenitrification == 1;
• Oxygen consumption during nitrification is done in the nitrogen module - [aed_nitrogen][Inorganic Nutrients: C/N/P/Si];
• Ammonium and nitrate uptake by phytoplankton phtosynthesis is done in the phytoplankton module - aed_phytoplankton;
• Ammonium and nitrate uptake by macroalgae phtosynthesis is done in the macroalgae module - aed_phytoplankton;
• Ammonium and nitrate release and/or consumption from the sediment can be managed via the sediment flux module - aed_sedflux;
• Ammonium and nitrate release and/or consumption from the sediment can be computed dynamically using the sediment diagnenesis module - aed_seddiagnesis;

6.3.5 Feedbacks to the Host Model

The nitrogen module has no feedbacks to the host hydrodynamic model.

6.4 Model Description - Adding N₂O Reactions

The basic function of the nitrogen model is described above, when the parameter simN2O is set to the number 0. Users may extend their model to simulate the N cycle in more detail, including resolution of intermediate N pools. Using these advanced options, there are extra reaction pathways that are not critical for resolving basic nutrient cycling processes, but are needed for calculating the concentration of the greenhouse gas N₂O.

Here, these advanced module options are outlined, for when the user sets the parameter simN2O to the number 1 or 2. Simulation option 1 includes N₂O, using a relatively simplistic assumption that N₂O passively “leaks out” as a by-product or is consumed during the traditional nitrification-denitrification reactions. Simulation option 2 is a more comprehensive biogeochemical depiction of N cycling between its different redox states and considering the full diversity of autotrophic and heterotrophic pathways.

In addition to different N reaction pathways in these sub-models, the inclusion of additional inorganic N components is also accompanied by new process pathways for atmospheric exchange and sediment interaction.

6.4.1 Process Descriptions (simN20 = 1)

The simN2O 1 option is based on the conceptual model from Babbin et al. or Nevison. If the parameter simN2O is set to the number 1, N₂O is both created and consumed through the denitrification reaction, and produced during nitrification; these rates are oxygen dependent.

The main balance equation for the additional N₂O is summarised as:

\[\begin{equation} \frac{\partial N_{2}O}{\partial t} = {f_{nitp}^{N_{2}O}} + {f_{denp}^{N_{2}O}} - {f_{denc}^{N_{2}O}} + \color{#394E73}{f_{atm}^{N_{2}O}} + \color{#8B701F}{f_{sed}^{N2O}} \tag{6.13} \end{equation}\]

6.4.1.1 Denitrification production of N₂O

All of the NO₃^- consumed by denitrification is assumed to first produces N₂O. The rate of production of N₂O is multiplied by half because there is one mole of N₂O produced for every two moles of NO₃^- consumed. The rate of denitrification is calculated as described here, and can have different O₂ limitations, using the parameter use_oxy.

\[\begin{equation} f^{N_{2}O}_{denp} = \frac{1}{2}f^{NO_{x}}_{denit} \tag{6.14} \end{equation}\]

6.4.1.2 Denitrification consumption of N₂O

Denitrification can also consume N₂O, when the N₂O acts as a high energy yielding oxidant that reacts with organic matter. The organic matter reaction is described in the organic matter model page here. The rate of N₂O consumption is calculated as shown in Equation (6.15). Rn2o is a kinetic rate constant that sets the speed of the reaction and Kn2oc is the parameter for the exponential O₂ inhibition of the reaction.

\[\begin{equation} f_{denc}^{N2O}=R_{N_{2}O} e^{(-O_2/{K_{N_2Oc}})} N_{2}O \tag{6.15} \end{equation}\]

6.4.1.3 Nitrification production of N₂O

N₂O is also produced by the O₂ oxidation of NH₄⁺ as:

6.4.1.4 Atmospheric N₂O Flux

N₂O fluxes from the atmosphere are calculated from the difference between water and atmospheric concentration:

\begin{equation} f_{atm}^{N_{2}O}=k_{N_{2}O}(N_{2}O-N_{2}O_{atm}) \end{equation}

Where \(N_{2}O_{atm}\) is the user defined atmospheric value, and \(k_{N_{2}O}\) is the piston velocity; refer to generic utility Section X for more detail using aed2_gas_piston_velocity, and the n2o_piston_model options.

6.4.1.5 Sediment N₂O Flux

N₂O flux from the sediment is calculated in a similar way to the fluxes of NO₃^- and NH₄⁺(Equation 22).

\begin{equation} \(f_{sed}^{N2O}=F_{sed}^{n2o} \theta_{sedamm}^{T-20}\Phi_{O2}^{n2o}\left[O_2\right]\) \end{equation}

\[ f_{sed}^{N_{2}O}=F_{sed}^{N_{2}O}\theta_{sedamm}^{T-20}\Phi_{O_{2}}^{N_{2}O}[O_2] \] {#eq:label}

6.4.2 Process Descriptions (simN2O = 2)

The simN2O 2 option uses the terminology from Weissbach et al. (2017) for the names of the reaction processes, in order to avoid the ambiguity found across publications. The model processes are described as being part of either the oxidation pathway or reduction pathway.

The main balance equations for the additional simulated variables are summarised as:

\[\begin{equation} \frac{\partial{NO}_3}{\partial t}=f_{Nitratation}-f_{Denitratation}+f_{atmdep}^{NOx}+f_{sed}^{NO3} \end{equation}\] \[\begin{equation} \frac{\partial{NO}_2}{\partial t}={f_{Nitritation}+f}_{Denitratation}-f_{Denitritation}+f_{sed}^{NO2} \end{equation}\] \[\begin{equation} \frac{\partial N_2O}{\partial t}=f_{Nitrousation}+f_{nitrous\ denitritation}-f_{denitrousation}+f_{atm}^{N2O}+f_{sed}^{N2O} \end{equation}\] \[\begin{equation} \frac{\partial{NH}_4}{\partial t}=f_{DNRA}+f_{NH4\ release}-f_{NH4\ \ oxidation}+f_{atmdep}^{NH4}+f_{sed}^{NH4} \end{equation}\]

6.4.2.1 Nitrogen Oxidation Pathways

In the oxidation pathway, reduced N in the form of ammonium is first oxidised to NO₂ and N₂O before NO₃, as seen in Figure 1. These processes are described next.

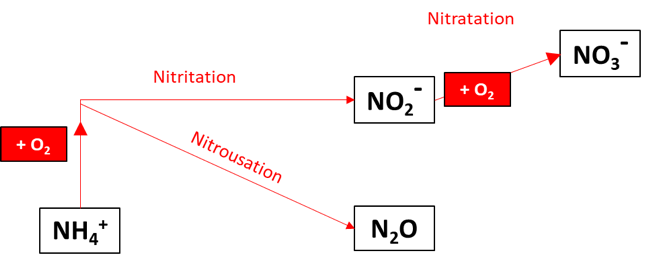
Figure 6.1: Nitrogen oxidation pathways resolved when simN2O=2.

6.4.2.2 Nitratation

Nitratation is the production of NO₃^- (nitrate) from NO₂^- by O₂ oxidation. The rate is calculated as a second-order reaction proportional to both NO₂^- and O₂ concentrations (Equation 14). The parameter Rno2o2 is the kinetic rate constant for the reaction.

\[\begin{equation} f_{Nitratation}=R_{{NO}_2O_2}\times{NO}_2^-\times O_2 \end{equation}\]

6.4.2.3 Ammonium oxidation

NH₄⁺ is oxidized by O₂ to both N₂O and NO₂^-. The rate of NH₄⁺ consumption is the second-order reaction proportional to both O₂ and NH₄⁺ concentrations (Equation 15). The parameter Rnh4o2 is the kinetic rate constant for the reaction.

\[\begin{equation} f_{Ammonium\ oxidation}=R_{{NH}_4O_2}\times{NH}_4^+\times O_2 \end{equation}\]

6.4.2.4 Nitritation

Nitritation is the production of NO₂^- (nitrite) under conditions of high O₂ concentration, from ammonium oxidation. It is limited by a partitioning function, in which the constant Kpart_ammox is the same as that for nitrousation, described below. Above a critical O₂ concentration, this reaction pathway is favoured (Equation 16). The term R~Ammonium oxidation~ refers to the rate equation described above, rather than a kinetic constant.

\[\begin{equation} f_{Nitritation}=f_{Ammonium\ oxidation}\frac{O_2}{K_{part\ ammox}^ +O_2} \end{equation}\]

6.4.2.5 Nitrousation

Nitrousation is one of two pathways that produce N₂O using simN2O set to the number 2 (the other pathway is the reduction of NO₂^- via nitrous denitritation). This process occurs under conditions of low O₂ concentration, and it is inhibited by oxygen, using an inhibition function (Equation 18). The constantKpart_ammox is the same as that in the nitritation process, which means that below a critical O₂ concentration, this reaction pathway is favoured over nitritation. The reaction is multiplied by half, because for each mole of NH₄⁺ oxidized, one mole of N₂O is produced. The term R~Ammonium oxidation~ refers to the rate equation described above, rather than a kinetic constant.

\[\begin{equation} f_{Nitrousation}=\frac{1}{2}f_{Ammonium\ oxidation}\frac{K_{part\ ammox}}{K_{part\ ammox} +O_2} \end{equation}\]

6.4.2.6 Organic matter oxidation - nitrogen reduction reactions

When the simN2O switch is set to 2, the complex set of N₂O reactions is used. The details of the organic matter processes are explained on the organic matter model page here. The five nitrogen processes are explained here.

6.4.2.7 Deammonification (anammox) pathway

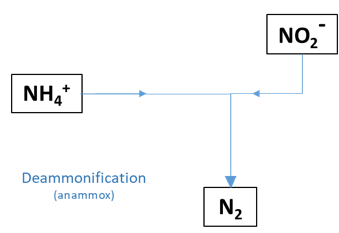
Figure 6.2: Anammox pathways.

The deammonification pathway is the oxidation of NH₄⁺ by NO₂^- to produce N₂. It uses neither organic matter nor O₂, although it is inhibited by the presence of O₂. This process is sometimes referred to as anammox (anaerobic ammonium oxidation), however, Weissbach et al (2017) use the term deammonification to distinguish it from the anammox commercial bioreactor. The parameter Rnh4no2 is the kinetic rate constant for this reaction. The parameter Kin_deamm is the O₂ concentration parameter for O₂ inhibition of this reaction.

\[\begin{equation} f_{deammonification}=R_{{NH}_4{NO}_2}\times{NO}_2^-\times{NH}_4^+\times\frac{K_{in\ deamm}}{K_{in\ deamm} +O_2} \end{equation}\]

6.4.3 Variable Summary

6.4.3.1 State variables

The following state variables are relevant to the nitrogen module, and dependent variables from other modules (Table x).

Symbol	Variable	AED identifier	Unit	Comment
aed_nitrogen
NO3-	Nitrate	NIT_nit	mmol m-3	simN2O=1,2
NO2-	Nitrite	NIT_no2	mmol m-3	simN2O=2 only
N2O	Nitrous oxide	NIT_n2o	mmol m-3	simN2O=1,2
NH4+	Ammonium	NIT_amm	mmol m-3	simN2O=1,2
N2	Dinitrogen	NIT_n2	mmol m-3	not tracked
Dependent variables
O2	Oxygen	OXY_oxy	mmol m-3
DOC	Dissolved organic carbon	OGM_doc	mmol m-3

6.4.3.2 Diagnostics variables

The following diagnostic variables are able to be output, based on the setting of diag_level>0 (Table x).

6.4.4 Parameter summary

An overview of the parameters used in the nitrogen module for users selecting simN2O 1 or 2, are summarised in Table X.

Parameter name	Description	Unit	Parameter type	Default	Typical range	Comment
simN2O	Switch to use simple or advanced N reactions		INTEGER	1	0, 1, 2
Rn2o	Kinetic rate constant for N2O consumption	s-1	AED_REAL	0.0015
Kn2oc	Exponential O2 inhibiting parameter for N2O consumption through denitrification	mmol m-3	AED_REAL	0.3
Knev	O2 threshold for switching on N2O production from nitrification	mmol m-3	AED_REAL	3
aa	O2 inhibition parameter	mmol m-3	AED_REAL	0.26
bb	O2 inhibition parameter		AED_REAL	-0.0006
simN2O	Switch to use simple or advanced N reactions		INTEGER	2	0, 1, 2
Rno2o2	Kinetic rate constant for nitratation	mmol-1 m3 s-1	AED_REAL	1
Rnh4o2	Kinetic rate constant for nitratation	mmol-1 m3 s-1	AED_REAL	1
Kpart_ammox	Partitioning parameter for the products of ammonium oxidation, based on O2 concentration	mmol m-3	AED_REAL	20
Rdom_minerl	Kinetic rate constant for DOC mineralisation	mmol-1 m3 s-1	AED_REAL	0.001		OGM
Kdom_minerl	O2 concentration for inhibition and limitation	mmol m-3	AED_REAL	0.886		OGM
theta_minerl	Temperature parameter		AED_REAL	1		OGM
f_an				1		OGM
`Klim_denitrousv	N2O concentration to limit denitrousation and to inhibit denitratation and denitritation	mmol m-3	AED_REAL	1
Kin_denitrousv	O2 concentration to inhibit denitrousation	mmol m-3	AED_REAL	0.205
Knit	NO3- concentration to limit denitratation	mmol m-3	AED_REAL	1
Kin_denitrat	O2 concentration for inhibiting denitratation	mmol m-3	AED_REAL	20
Klim_denitrit	NO2- concentration parameter that inhibits denitratation and limits denitritation	mmol m-3	AED_REAL	1
Kpart_denitrit	Partitioning parameter for the products of denitritation	mmol m-3	AED_REAL	1
simN2O	Switch to use simple or advanced N reactions		INTEGER	2	0, 1, 2
Rnh4no2	Kinetic rate constant for deammonification	mmol-1 m3 s-1	AED_REAL	1
Kin_deamm	O2 concentration for inhibition of deammonification	mmol m-3	AED_REAL	0.886
simN2O	Switch to use simple or advanced N reactions		INTEGER	1 or 2	0, 1, 2
atm_n2o	Atmospheric N2O concentration	mmol m-3 or ppm	AED_REAL	0.32×10-6
simN2O	Switch to use simple or advanced N reactions		INTEGER	1 or 2	0, 1, 2
use_oxy
Fsed_n2o	Maximum N2O sediment flux rate	mmol m-2 y-1		0
Ksed_n2o	O2 inhibition concentration parameter	mmol m-2 y-1	AED_REAL	30
theta_sed_n2o	Temperature limiting factor for sediment N2O flux		AED_REAL	1

6.4.5 Optional Module Links

As with the default model, other nitrogen sources/sinks are indicated in Eq s… . These include:

• Ammonium release during bacterial mineralisation of DON in the organic matter module - aed_organic_matter;
• Nitrate consumption during denitrification of DON in the organic matter module - done in aed_organic_matter if simDenitrification == 1;
• Oxygen consumption during nitrification is done in the nitrogen module - [aed_nitrogen][Inorganic Nutrients: C/N/P/Si];
• Ammonium and nitrate uptake by phytoplankton phtosynthesis is done in the phytoplankton module - aed_phytoplankton;
• Ammonium and nitrate uptake by macroalgae phtosynthesis is done in the macroalgae module - aed_phytoplankton;
• Ammonium and nitrate release and/or consumption from the sediment can be managed via the sediment flux module - aed_sedflux;
• Ammonium and nitrate release and/or consumption from the sediment can be computed dynamically using the sediment diagnenesis module - aed_seddiagnesis;

6.4.6 Feedbacks to the Host Model

This nitrogen module configuration also contains no feedbacks to the host hydrodynamic model.

6.5 Setup & Configuration

An example aed.nml parameter specification block for the aed_nitrogen module is shown below:

&aed_nitrogen
  !-- Initial values
   amm_initial = 2.6
   nit_initial = 0.1
   n2o_initial = 0.1
  !-- Nitrification
   Rnitrif =  0.01358676
   Knitrif = 62.02209
   theta_nitrif = 1.08
   nitrif_reactant_variable = 'OXY_oxy'
   nitrif_ph_variable = ''
   simNitrfpH = .false.
   Rnh4o2 = 1.0
   Rno2o2 = 1.0
  !-- N2O reactions
   simN2O = 0
   Rn2o = 0.05
   Kpart_ammox = 1.0
   Kin_deamm = 1.0
   atm_n2o = 3.2e-07
   n2o_piston_model = 4
  !-- Annamox
   Rnh4no2 = 0.001
   kanammox = 0.001
   Kanmx_nit = 1.320344
   Kanmx_amm = 0.8666655
  !-- De-nitrification
   Rdenit = 9.968717
   Kdenit = 29.86566
   theta_denit = 1.062862
   Rdnra = 0.01123021
   Kdnra_oxy = 0.360534
  !-- Atmospheric deposition
   simDryDeposition = .true.
   atm_din_dd = 0.5
   simWetDeposition = .true.
   atm_din_conc = 0.5
  !-- Sediment fluxes
   Ksed_amm = 41.25
   Ksed_nit = 73.26015
   Fsed_n2o = 0
   Ksed_n2o = 100
   theta_sed_amm = 1.068994
   theta_sed_nit = 1.068994
   Fsed_amm         =   1.0
   Fsed_nit         =  -0.05
 ! Fsed_amm_variable = 'SDF_Fsed_amm'
 ! Fsed_nit_variable = 'SDF_Fsed_nit'
/

6.6 Case Studies & Examples

6.6.1 Case Study: Yarra River Estuary

Bruce et al. (2015) demonstrate the base nitrogen setup in a 3D model of Yarra River estuary, an urban riverine estuary in Melbourne, Australia, that experiences dynamic movement of a hypoxic salt-wedge based on river flow and tidal interactions.

The results of the simulation are shown in Figure X, highlighting the change in surface and bottom NH4, NO3 and organic nitrogen pools along the estuary length.

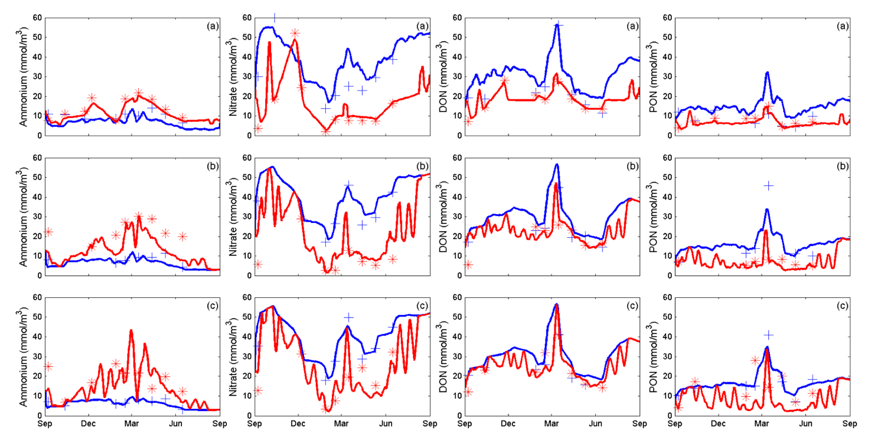
Figure 6.3: Time series data for surface (blue) and bottom (red) ammonium, nitrate, dissolved and particulate organic nitrogen for (a) Morell Bridge, (b) Scotch College, (c) Bridge Road. Crosses and asterisks represent observed data for surface and bottom concentrations respectively and solid lines simulated data.

6.6.2 Publications

Author/Year	Paper Title	Description
Bruce et al. (2015)	A model of oxygen and nitrogen biogeochemical response to hydrodynamic regimes in the Yarra River estuary	NA
Huang et al. (2019)	An integrated modelling system for water quality forecasting in an urban eutrophic estuary: The Swan-Canning Estuary virtual observatory	NA

References

Huang, P., Trayler, K., Wang, B., Saeed, A., Oldham, C.E., Busch, B., Hipsey, M.R., 2019. An integrated modelling system for water quality forecasting in an urban eutrophic estuary: The swan-canning estuary virtual observatory, Journal of Marine Systems 199, 103218. https://doi.org/10.1016/j.jmarsys.2019.103218