10 Phytoplankton
10.2 Overview
The approach to simulate algal biomass is to adopt several plankton functional types (“PFT’s”) that are typically defined based on specific groups such as diatoms, dinoflagellates and cyanobacteria. Whilst each group that is simulated is unique, they share a common mathematical approach and each simulate growth, death and sedimentation processes, and customisable internal nitrogen, phosphorus and/or silica stores if desired. Distinction between groups is made by adoption of groups specific parameters for environmental dependencies, and/or enabling options such as vertical migration or N fixation.
10.3 Model Description
The main balance equation for a single configured phytoplankton group, \(PHY_a\), is described as:
\[\begin{eqnarray} \frac{D}{Dt}PHY_{a} = \color{darkgray}{ \mathbb{M} + \mathcal{S} } \quad &+& \overbrace{ f_{gpp}^{PHY_{a}} - f_{rsp}^{PHY_{a}} - f_{mor}^{PHY_{a}} - f_{exc}^{PHY_{a}} + f_{set}^{PHY_{a}} + \hat{f}_{res}^{PHY_{a}} }^\text{aed_phytoplankton} \\ \tag{10.1} &-& \color{brown}{ f_{grz}^{ZOO} - \hat{f}_{grz}^{BIV} } \\ \nonumber \end{eqnarray}\]
where \(\mathbb{M}\) and \(\mathcal{S}\) refer to water mixing and boundary source terms, respectively. The main processes controlling the rate of phytoplanklton biomass accumulation are gross primary productivity, respiration, mortality, excretion and exudation, settling and vertical migration, and resuspension. In addition, the coloured \(\color{brown}{f}\) terms reflect phytoplankton related fluxes computed by other (optionally) linked modules such as the zooplankton (\(\mathrm{ZOO}\)) or bivalve (\(\mathrm{BIV}\)) modules, which compute grazing/filtration fluxes based on their rate of phytoplankton consumption.
The default method for simulating phytoplankton biomass assess a constant intracellular C:N:P ratio. In this case, only a single state variable for carbon biomass is simulated and subject to trasnport, with the N and P content computed based on the C concentration at any point in time or space. The module also supports the simulation of dynamic intracellular stoichiometry should this be required. Within this setting, state variables are also optionally created for phytoplankton biomass N and P content (termed \(IN\) and \(IP\), respectively):
\[\begin{eqnarray} \frac{D}{Dt}IN_{a} = \color{darkgray}{ \mathbb{M} + \mathcal{S} } \quad &+& \overbrace{ f_{upt}^{IN_{a}} - f_{rsp}^{IN_{a}} - f_{mor}^{IN_{a}} - f_{exc}^{IN_{a}} + f_{set}^{IN_{a}} + \hat{f}_{res}^{IN_{a}} }^\text{aed_phytoplankton} \\ \tag{10.2} &-& \color{brown}{ f_{grz}^{ZOO} - \hat{f}_{grz}^{BIV} } \\ \nonumber \end{eqnarray}\] and \[\begin{eqnarray} \frac{D}{Dt}IP_{a} = \color{darkgray}{ \mathbb{M} + \mathcal{S} } \quad &+& \overbrace{ f_{upt}^{IP_{a}} - f_{rsp}^{IP_{a}} - f_{mor}^{IP_{a}} - f_{exc}^{IP_{a}} + f_{set}^{IP_{a}} + \hat{f}_{res}^{IP_{a}} }^\text{aed_phytoplankton} \\ \tag{10.3} &-& \color{brown}{ f_{grz}^{ZOO} - \hat{f}_{grz}^{BIV} } \\ \nonumber \end{eqnarray}\]
A detailed overview of the above functions for C, N and P for each of the various process rates is provided next.
10.3.1 Process Descriptions
Photosynthesis & Nutrient Uptake
For each phytoplankton group, \(a\), the maximum potential growth rate at 20˚C is multiplied by the minimum value of expressions for limitation by light, phosphorus, nitrogen and silica (when configured). While there may be some interaction between limiting factors, a minimum expression is likely to provide a realistic representation of growth limitation (Rhee and Gotham, 1981). Therefore, photosynthesis is parameterized as the uptake of carbon, and depends on the temperature, light and nutrient dimensionless functions (adopted from Hipsey & Hamilton, 2008; Li et al., 2013):
\[\begin{equation} \text{Phytoplankton Growth Equation} \tag{10.4} \end{equation}\] \[\begin{align} {f_{gpp}^{PHY_{a}}} &= \: [PHY_{a}] \times \end{align}\] \[\begin{align} \underbrace{{R_{growth}^{PHY_{a}}}}_{\text{Max growth rate at 20˚C}} \times \underbrace{(1-{k_{pr}^{PHY_{a}}})}_{\text{Photorespiratory loss}} \times \underbrace{{\Phi_{tem}^{PHY_{a}}}(T)}_{\text{Temperature scaling}} \times \underbrace{{\Phi_{str}^{PHY_{a}}}(T)}_{\text{Metabolic stress}} \times \end{align}\] \[\begin{align} &{\text{min}}\begin{Bmatrix}\underbrace{\Phi_{light}^{PHY_{a}}(I)}_{\text{Light limitation}},\underbrace{\Phi_{N}^{PHY_{a}}(NO_{3},NH_{4},PHY_{N_{a}})}_{\text{N limitation}},\underbrace{\Phi_{P}^{PHY_{a}}(PO_{4},PHY_{P_{a}})}_{\text{P limitation}},\underbrace{\Phi_{Si}^{PHY_{a}}(RSi)}_{\text{Si limitation}}\end{Bmatrix} \times \end{align}\]
\[\begin{equation} \Phi_{tem}^{{PHY}_a}\left(T\right)=\vartheta_a^{T-20}-\vartheta_a^{k\left[T-{c1}_a\right]}+{c0}_a \tag{10.5} \end{equation}\]
where \({c1}_a\) and \({c0}_a\) are solved numerically given input values of: \(T_a^{std}\), \(T_a^{opt}\) and \(T_a^{max}\).
Light limitation: The level of light limitation on phytoplankton growth can be modelled as photoinhibition or non-photoinhibition. In the absence of significant photoinhibition, Webb et al. (1974) suggested a relationship for the fractional limitation of the maximum potential rate of carbon fixation for the case where light saturation behavior was absent (Talling, 1957), and the equations can be analytically integrated with respect to depth (Hipsey and Hamilton, 2008). For the case of photoinhibition, the light saturation value of maximum production (\(I_S\)) is used and the net level effect can be averaged over the cell by integrating over depth.
The aed_phytoplankton module contains several light functions, including those from a recent review by Baklouti et al. (2006). The user must select the sensitivity to light according to a photosynthesis-irradiance (P-I curve) formulation and each species must be set to be either non-photoinhibited or photoinhibited according to the options in Table 9.
Figure 10.1: Light limitation of pytoplankton via various model approaches.
Nutrient limitation: Limitation of the photosynthetic rate may be dampened according to nitrogen or phosphorus availability, and this is either approximated using a Monod expression of the static model is chosen, or based on the internal nutrient stoichiometry if the dynamic (Droop uptake) model is selected: For advanced users, an optional metabolic scaling factor can be included to reduce the photosynthetic capacity of the simulated organisms, for example due to metabolic stress due to undertaking N2 fixation:\[\begin{equation} \Phi_{str}^{{PHY}_a}=\underbrace{f_{NF}^{{PHY}_a}+\left[{1-f}_{NF}^{{PHY}_a}\right]\Phi_N^{{PHY}_a}\left({NO}_3,{NH}_4,{PHY_N}_a\right)}_{N_{2}\text{ fixation growth scaling}} \tag{10.6} \end{equation}\]
The above discussion relates to photosynthesis and carbon uptake by the phytoplankton community. In addition users must choose one of two options to model the P, N uptake dynamics for each algal group: i) a constant nutrient to carbon ratio, or ii) simulation of dynamic intracellular stores. For the first model a simple Michaelis-Menten equation is used to model nutrient limitation with a half-saturation constant for the effect of external nutrient concentrations on the growth rate.
The internal phosphorus and nitrogen dynamics within the phytoplankton groups can be modelled using dynamic intracellular stores that are able to regulate growth based on the model of Droop (1974). This model allows for the phytoplankton to have dynamic nutrient uptake rates with variable internal nutrient concentrations bounded by user-defined minimum and maximum values (e.g., see Li et al., 2013).
The uptake of nitrogen must be partitioned into uptake of NO3, and NH4. The distinction between uptake of NO3 and NH4 is calculated automatically via a preference factor:\[\begin{equation} {\ p}_{NH4}^{{PHY}_a}=\frac{{NO}_3\ {NH}_4}{\left({NH}_4+K_N^{{PHY}_a}\right)\left({NO}_3+K_N^{{PHY}_a}\right)}\frac{{NH}_4{\ K}_N^{{PHY}_a}}{\left({NH}_4+{NO}_3\right)\left({NO}_3+K_N^{{PHY}_a}\right)} \tag{10.7} \end{equation}\]
\[\begin{equation} p_{NO3}^{{PHY}_a}=1-{\ p}_{NH4}^{{PHY}_a} \tag{10.8} \end{equation}\]
For diatom groups, silica processes are simulated that include uptake of dissolved silica. The silica limitation function for diatoms is similar to the constant cases for nitrogen and phosphorus which assumes a fixed C:Si ratio.
Respiration, Excretion & Mortality
Metabolic loss of nutrients from mortality and excretion is proportional to the internal nitrogen to chla ratio multiplied by the loss rate and the fraction of excretion and mortality that returns to the detrital pool. Loss terms for respiration, natural mortality and excretion are modelled with a single ‘respiration’ rate coefficient. This loss rate is then divided into the pure respiratory fraction and losses due to mortality and excretion. The constant \(f_{DOM}\) is the fraction of mortality and excretion to the dissolved organic pool with the remainder into the particulate organic pool. Nutrient losses through mortality and excretion for the internal nutrient model are similar to the simple model described above, except that dynamically calculated internal nutrient concentrations are used.
\[\begin{align*} \hat{R}&=R_{resp}^{{PHY}_a}\ \ \Phi_{sal}^{{PHY}_a}\left(S\right)\ \ \left(\vartheta_{resp}^{{PHY}_a}\right)^{T-20} \tag{10.9}\\ f_{resp}^{{PHY_C}_a}&=k_{fres}^{{PHY}_a}\ \hat{R}\ \left[{PHY_C}_a\right] \tag{10.10}\\ f_{excr}^{{PHY_C}_a}&=\left(1-k_{fres}^{{PHY}_a}\right)\ k_{fdom}^{{PHY}_a}\ \hat{R}\ \ \left[{PHY_C}_a\right] \tag{10.11}\\ f_{mort}^{{PHY_C}_a}&=\left(1-k_{fres}^{{PHY}_a}\right)\ \left({1-k}_{fdom}^{{PHY}_a}\right)\ \hat{R}\ \left[{PHY_C}_a\right] \tag{10.12}\\ f_{excr}^{{PHY_N}_a}&=k_{fdom}^{{PHY}_a}\ \hat{R}\ \left[{PHY_N}_a\right] \tag{10.13}\\ f_{mort}^{{PHY_N}_a}&=\left(1-k_{fdom}^{{PHY}_a}\right)\ \hat{R}\ \left[{PHY_N}_a\right] \tag{10.14}\\ f_{excr}^{{PHY_P}_a}&=k_{fdom}^{{PHY}_a}\ \hat{R}\ \left[{PHY_P}_a\right] \tag{10.15}\\ f_{mort}^{{PHY_P}_a}&=\left(1-k_{fdom}^{{PHY}_a}\right)\ \hat{R}\ \ \left[{PHY_P}_a\right] \tag{10.16}\\ f_{excr}^{{PHY_{Si}}_a}&=\hat{R}\ \left[{PHY_{Si}}_a\right] \tag{10.17} \end{align*}\]
The salinity effect on mortality is given by various quadratic formulations, depending on the groups sensitivity to salinity (Griffin et al 2001; Robson and Hamilton, 2004). An example of the use of various salinity limitation options is shown in Figure 3.
Figure 10.1: Salinity growth suppression of pytoplankton via various model approaches.
Figure 10.1: Salinity respiration amplification of pytoplankton via various model approaches.
10.3.2 Optional Module Links
Other modules can influence phytoplankton sources/sinks, as indicated in Eq (10.1) for \(PHY\). These include:
- aed_oxygen: \(O_2\) is influenced by the rate of photosynthesis and respiration.
- aed_carbon: \(DIC\) is influenced by the rate of photosynthesis and respiration.
- aed_phosphorus: \(PO_4\) is consumed during photosynthesis.
- aed_nitrogen: \(NO_3\) and \(NH_4\) are consumed during photosynthesis.
- aed_silica: \(SiO2\) is consumed during photosynthesis.
- aed_organic_matter: \(DOM\) and \(POM\) is contributed to by the rate of phytoplankton excretion and mortality.
- aed_zooplankton: zooplankton can optionally graze upon any phytoplankton groups.
- aed_bivalve: bivalves can optionally graze upon any phytoplankton groups.
- aed_noncohesive: optional link to simulate the phytoplankton resuspension.
- aed_seddiagenesis: benthic phytoplankton (MPB) can grow and influence oxygen, carbon and nutrient fluxes at the sediment-water interface.
10.3.3 Feedbacks to the Host Model
The phytoplankton module can feedback conditions to the hydrodynamic model by modifying the light extinction coefficient. For each group simulated a specific attenuation coefficient, \(K_e\), is applied, and is specific for each group simulated.
This total light extinction computed by the PHY model is:
\[\begin{equation}
K_{d}^{phy} = \sum_{a}K_{e_{PHY_a}} PHY_a
\end{equation}\]
10.3.4 Variable Summary
The default variables created by this module, and the optionally required linked variables needed for full functionality of this module are summarised in Table 10.1. The diagnostic outputs able to be output are summarised in Table 10.2.
State Variables
| AED name | Symbol | Description | Unit | Type | Typical Range | Comments |
|---|---|---|---|---|---|---|
| aed_phytoplankton | ||||||
PHY_{group}
|
\[\mathbf{PHY}\] |
phytoplanton group water column concentration
|
\[\small{mmol\: C/m^3}\] | pelagic | 0-1000 |
select group using index from aed_phyto_pars database
|
PHY_{group}_IN
|
\[\mathbf{PHY_N}\] |
internal nitrogen concentration of phytoplakton group
|
\[\small{mmol\: N/m^3}\] | pelagic | 0 - 200 |
activated when simINDynamics \(\gt 1\)
|
PHY_{group}_IP
|
\[\mathbf{PHY_P}\] |
internal phosphorus concentration of phytoplakton group
|
\[\small{mmol\: P/m^3}\] | pelagic | 0-20 |
activated when simIPDynamics \(\gt 1\)
|
PHY_{group}_rho
|
\[\mathbf{PHY_{\rho}}\] | phytoplankton group mean cell density | \[\small{kg\: C/m^3}\] | pelagic | 900-1200 |
activated for a group when settling=3
|
PHY_mpb
|
\[\mathbf{MPB}\] | coarse particulate organic matter | \[\small{mmol\: C/m^2}\] | benthic | 0-5000 |
activated when do_mpb \(\gt 0\)
|
| Dependent variables | ||||||
CAR_dic
|
\[\mathbf{DIC}\] | dissolved inorganic carbon concentration | \[\small{mmol\: C/m^3}\] | pelagic | NA | optionally linked |
NIT_amm
|
\[\mathbf{NH_4}\] | dissolved ammonium concentration | \[\small{mmol\: N/m^3}\] | pelagic | NA | optionally linked |
PHS_frp
|
\[\mathbf{PO_4}\] | dissolved phosphate concentration | \[\small{mmol\: P/m^3}\] | pelagic | NA | optionally linked |
OXY_oxy
|
\[\mathbf{O_2}\] | dissolved oxygen concentration | \[\small{mmol\: O_2/m^3}\] | pelagic | 0 - 500 | optionally linked |
NIT_nit
|
\[\mathbf{NO_3}\] | dissolved nitrate concentration | \[\small{mmol\: N/m^3}\] | pelagic | NA | optionally linked |
OGM_doc
|
\[\mathbf{DOC}\] | dissolved organic carbon concentration | \[\small{mmol\: C/m^3}\] | pelagic | 0 - 5000 | optionally linked |
OGM_poc
|
\[\mathbf{POC}\] | particulate organic carbon concentration | \[\small{mmol\: C/m^3}\] | pelagic | NA | optionally linked |
OGM_don
|
\[\mathbf{DON}\] | dissolved organic nitrogen concentration | \[\small{mmol\: N/m^3}\] | pelagic | NA | optionally linked |
OGM_pon
|
\[\mathbf{PON}\] | particulate organic nitrogen concentration | \[\small{mmol\: N/m^3}\] | pelagic | NA | optionally linked |
OGM_dop
|
\[\mathbf{DOP}\] | dissolved organic phosphorus concentration | \[\small{mmol\: P/m^3}\] | pelagic | NA | optionally linked |
OGM_pop
|
\[\mathbf{POP}\] | particulate organic phosphorus concentration | \[\small{mmol\: P/m^3}\] | pelagic | NA | optionally linked |
SIL_rsi
|
\[\mathbf{RSi}\] | reactive silica concentration | \[\small{mmol\: Si/m^3}\] | pelagic | NA | optionally linked |
NCS_resus
|
\[\mathbf{\mathcal{F}}_{resus}\] | sediment resuspension rate | \[\small{g/m^2/s}\] | benthic | 0 - 10 |
required for PHY resuspension, set via resus_link
|
Diagnostics
| AED name | Symbol | Description | Unit | Type | Typical Range | Comments |
|---|---|---|---|---|---|---|
| diag_level = 0+ | ||||||
PHY_set
|
\[\mathbf{f_{set}^{\mathbb{PHY}}}\] | phytoplankton community sedimentation flux | \[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
PHY_res
|
\[\mathbf{\hat{f}_{res}^{\mathbb{PHY}}}\] | phytoplankton community resuspension flux | \[\small{mmol\: C/m^2/d}\] | pelagic | NA | |
PHY_gpp
|
\[\mathbf{f_{gpp}^{\mathbb{PHY}}}\] | gross phytoplankton community primary production rate | \[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
PHY_ncp
|
\[\mathbf{f_{gpp}^{\mathbb{PHY}}} - \mathbf{f_{rsp}^{\mathbb{PHY}}}\] | net phytoplankton community production | \[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
| diag_level = 1+ | ||||||
PHY_upt_no3
|
\[\mathbf{f_{upt_{NO3}}^{\mathbb{PHY}}}\] | phytoplankton community \(NO_3\) uptake rate | \[\small{mmol\: N/m^3/d}\] | pelagic | NA | |
PHY_upt_nh4
|
\[\mathbf{f_{upt_{NH4}}^{\mathbb{PHY}}}\] | phytoplankton community \(NH_4\) uptake rate | \[\small{mmol\: N/m^3/d}\] | pelagic | NA | |
PHY_upt_n2
|
\[\mathbf{f_{upt_{N2}}^{\mathbb{PHY}}}\] | phytoplankton community \(N_2\) uptake rate | \[\small{mmol\: N/m^3/d}\] | pelagic | NA | |
PHY_upt_po4
|
\[\mathbf{f_{upt_{PO4}}^{\mathbb{PHY}}}\] | phytoplankton community \(PO_4\) uptake rate | \[\small{mmol\: P/m^3/d}\] | pelagic | NA | |
PHY_upt_dic
|
\[\mathbf{f_{upt_{DIC}}^{\mathbb{PHY}}}\] | phytoplankton community \(CO_2\) uptake rate | \[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
PHY_tchla
|
\[\mathbf{\mathbb{TCHLA}}\] | total chlorophyll-a concentration | \[\small{\mu g \, /L}\] | pelagic | NA | |
PHY_in
|
\[\mathbf{\mathbb{IN}}\] | total phytoplankton nitrogen concentration | \[\small{mmol\: N/m^3}\] | pelagic | NA | |
PHY_ip
|
\[\mathbf{\mathbb{IP}}\] | total phytoplankton phosphorus concentration | \[\small{mmol\: P/m^3}\] | pelagic | NA | |
PHY_mpb_ben
|
\[\mathbf{MPB}\] | microphytobenthos concentration | \[\small{mmol\: C/m^2}\] | benthic | 0 - 10000 |
activated when do_mpb >0
|
PHY_mpb_gpp
|
\[\hat{f}_{gpp}^{MPB}\] | benthic phytoplankton primary production | \[\small{mmol\: C/m^2/d}\] | benthic | NA |
activated when do_mpb >0
|
PHY_mpb_rsp
|
\[\hat{f}_{rsp}^{MPB}\] | benthic phytoplankton net production | \[\small{mmol\: C/m^2/d}\] | benthic | NA |
activated when do_mpb >0
|
PHY_mpb_swi
|
\[\hat{f}_{swi}^{MPB}\] | microphytobenthos vertical exchange | \[\small{mmol\: C/m^2/d}\] | benthic | NA |
activated when do_mpb >0
|
| diag_level = 10+ | ||||||
PHY_{name}_NtoP
|
\[\mathbf{\chi_{N:P}^{PHY}}\] |
phytoplankton internal N:P ratio for the \(a^{th}\) group, name
|
\[\small{-}\] | pelagic | NA | |
PHY_{name}_vvel
|
\[\mathbf{\omega_{p}^{PHY_a}}\] |
phytoplankton sedimentation velocity for the \(a^{th}\) group, name
|
\[\small{m/d}\] | pelagic | NA | |
PHY_{name}_gpp_c
|
\[\mathbf{f_{gpp}^{PHY_a}}\] |
phytoplankton gross primary production for the \(a^{th}\) group, name
|
\[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
PHY_{name}_rsp_c
|
\[\mathbf{f_{rsp}^{PHY_a}}\] |
phytoplankton respiration rate for the \(a^{th}\) group, name
|
\[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
PHY_{name}_exc_c
|
\[\mathbf{f_{exc}^{PHY_a}}\] |
phytoplankton excretion rate for the \(a^{th}\) group, name
|
\[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
PHY_{name}_mor_c
|
\[\mathbf{f_{mor}^{PHY_a}}\] |
phytoplankton mortality rate for the \(a^{th}\) group, name
|
\[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
PHY_{name}_set_c
|
\[\mathbf{f_{set}^{PHY_a}}\] |
phytoplankton sedimentation rate for the \(a^{th}\) group, name
|
\[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
PHY_{name}_gpp_n
|
\[\mathbf{f_{gpp}^{IN_a}}\] |
phytoplankton gross primary production for the \(a^{th}\) group, name
|
\[\small{mmol\: N/m^3}\] | pelagic | NA | |
PHY_{name}_rsp_n
|
\[\mathbf{f_{rsp}^{IN_a}}\] |
phytoplankton respiration rate for the \(a^{th}\) group, name
|
\[\small{mmol\: N/m^3}\] | pelagic | NA | |
PHY_{name}_exc_n
|
\[\mathbf{f_{exc}^{IN_a}}\] |
phytoplankton excretion rate for the \(a^{th}\) group, name
|
\[\small{mmol\: N/m^3}\] | pelagic | NA | |
PHY_{name}_mor_n
|
\[\mathbf{f_{mor}^{IN_a}}\] |
phytoplankton mortality rate for the \(a^{th}\) group, name
|
\[\small{mmol\: N/m^3}\] | pelagic | NA | |
PHY_{name}_set_n
|
\[\mathbf{f_{set}^{IN_a}}\] |
phytoplankton sedimentation rate for the \(a^{th}\) group, name
|
\[\small{mmol\: N/m^3}\] | pelagic | NA | |
PHY_{name}_gpp_p
|
\[\mathbf{f_{gpp}^{IP_a}}\] |
phytoplankton gross primary production for the \(a^{th}\) group, name
|
\[\small{mmol\: P/m^3/d}\] | pelagic | NA | |
PHY_{name}_rsp_p
|
\[\mathbf{f_{rsp}^{IP_a}}\] |
phytoplankton respiration rate for the \(a^{th}\) group, name
|
\[\small{mmol\: P/m^3/d}\] | pelagic | NA | |
PHY_{name}_exc_p
|
\[\mathbf{f_{exc}^{IP_a}}\] |
phytoplankton excretion rate for the \(a^{th}\) group, name
|
\[\small{mmol\: P/m^3/d}\] | pelagic | NA | |
PHY_{name}_mor_p
|
\[\mathbf{f_{mor}^{IP_a}}\] |
phytoplankton mortality rate for the \(a^{th}\) group, name
|
\[\small{mmol\: P/m^3/d}\] | pelagic | NA | |
PHY_{name}_set_p
|
\[\mathbf{f_{set}^{IP_a}}\] |
phytoplankton sedimentation rate for the \(a^{th}\) group, name
|
\[\small{mmol\: P/m^3/d}\] | pelagic | NA | |
PHY_{name}_fI
|
\[\mathbf{\Phi_{light}^{PHY_{a}}}\] |
phytoplankton growth limitation function for the \(a^{th}\) group, name
|
\[\small{-}\] | pelagic | 0 - 1 | |
PHY_{name}_fNit
|
\[\mathbf{\Phi_{N}^{PHY_{a}}}\] |
phytoplankton growth limitation function for the \(a^{th}\) group, name
|
\[\small{-}\] | pelagic | 0 - 1 | |
PHY_{name}_fPho
|
\[\mathbf{\Phi_{P}^{PHY_{a}}}\] |
phytoplankton growth limitation function for the \(a^{th}\) group, name
|
\[\small{-}\] | pelagic | 0 - 1 | |
PHY_{name}_fSil
|
\[\mathbf{\Phi_{Si}^{PHY_{a}}}\] |
phytoplankton growth limitation function for the \(a^{th}\) group, name
|
\[\small{-}\] | pelagic | 0 - 1 | |
PHY_{name}_fT
|
\[\mathbf{\Phi_{tem}^{PHY_{a}}}\] |
phytoplankton growth limitation function for the \(a^{th}\) group, name
|
\[\small{-}\] | pelagic | 0 - 1.5 | |
PHY_{name}_fSal
|
\[\mathbf{\Phi_{sal}^{PHY_{a}}}\] |
phytoplankton growth limitation function for the \(a^{th}\) group, name
|
\[\small{-}\] | pelagic | 0 - 5 | |
PHY_tphy
|
\[\mathbf{TPHY}\] | total phytoplankton community, \(\mathbb{PHY}\) concentration | \[\small{mmol\: C/m^3/d}\] | pelagic | NA | |
PHY_ppr
|
\[\mathbf{f_{gpp}^{\mathbb{PHY}}} / \mathbf{f_{rsp}^{\mathbb{PHY}}}\] | gross phytoplankton \(P:R\) ratio | \[\small{-}\] | pelagic | NA | |
PHY_npr
|
\[\mathbf{f_{ncp}^{\mathbb{PHY}}} / \mathbf{f_{rsp}^{\mathbb{PHY}}}\] | net phytoplankton P:R ratio | \[\small{-}\] | pelagic | NA | |
PHY_par
|
\[\mathbf{I_{PAR}}\] | photosynthetically active radiation | \[\small{W/m^2}\] | pelagic | 0-1200 | |
10.3.5 Parameter and Option Summary
The module requires users to set both module level confiuration options and parameters, and group-specific parameters.
The group-specific parameters and settings are read in through the aed_phyto_pars, summarised in Table 10.3.
| AED name | Symbol | Description | Unit | Type | Typical Range | Comments |
|---|---|---|---|---|---|---|
| General | ||||||
p_name
|
\[a\] | name of phytoplankton group | \[\small{-}\] | string |
|
user specified name of chosen phytoplankton group, \(a\) |
p_initial
|
\[PHY |_{t=0}\] | initial concentration of phytoplankton | \[\small{mmol\: C/m^3}\] | float | 0-1000 | can be overwritten by initial condition files |
p0
|
\[PHY_0\] | minimum concentration of phytoplankton | \[\small{mmol\: C/m^3}\] | float | 1-20 |
|
Xcc
|
\[\chi_{C:chla}^{PHY}\] | carbon to chlorophyll ratio | \[\small{mg\: C/mg\: chla}\] | float | 10 - 1000 |
|
| Growth | ||||||
R_growth
|
\[R_{growth}^{PHY}\] | phytoplankton group maximum growth rate at \(20^{\circ}C\) | \[\small{/d}\] | float | 0.1 - 5.0 |
|
fT_Method
|
\[\Theta_{tem}^{phy}\] | specifies temperature limitation function of growth | \[\small{-}\] | integer | 0-1 | 0 = no temperature limitation 1= CAEDYM style |
theta_growth
|
\[\theta_{growth}^{phy}\] | Arrenhius temperature scaling for growth function | \[\small{-}\] | float | 1 - 1.2 |
|
T_std
|
\[T_{std}\] | standard temperature | \[\small{^{\circ}C}\] | float | 20 |
|
T_opt
|
\[T_{opt}\] | optimum temperature | \[\small{^{\circ}C}\] | float | NA |
|
T_max
|
\[T_{max}\] | maximum temperature | \[\small{^{\circ}C}\] | float | NA |
|
| Light | ||||||
lightModel
|
\[\Theta_{lgt}^{phy}\] | switch to assign the type of light response function | \[\small{-}\] | integer | 0-1 |
|
I_K
|
\[I_K\] | half saturation constant for light limitation of growth | \[\small{W/m^2}\] | float | NA | used if \(\Theta_{lgt}^{phy}\) is 0 |
I_S
|
\[I_S\] | saturating light intensity for optimum photosynthesis | \[\small{W/m^2}\] | float | NA | used if \(\Theta_{lgt}^{phy}\) is 1 |
KePHY
|
\[K_e\] | specific attenuation coefficient | \[\small{/m/(mmol\:C/m^3)}\] | float | NA |
|
| Respiration | ||||||
f_pr
|
\[f_{pr}\] | fraction of primary production lost to exudation | \[\small{-}\] | float | NA |
|
R_resp
|
\[R_{resp}^{PHY}\] | phytoplankton respiration/metabolic loss rate at \(20^{\circ}C\) | \[\small{/d}\] | float | 0.01 - 0.3 |
|
theta_resp
|
\[\theta_{resp}^{phy}\] | Arrhenius temperature scaling factor for respiration | \[\small{-}\] | float | 1 - 1.2 |
|
k_fres
|
\[k_{fres}\] | fraction of metabolic loss that is true respiration | \[\small{-}\] | float | 0 - 1 |
|
k_fdom
|
\[k_{fdom}\] | fraction of metabolic loss that is released as DOM | \[\small{-}\] | float | 0 - 1 |
|
| Salinity | ||||||
salTol
|
\[\Theta_{sal}^{phy}\] | type of salinity limitation function | \[\small{-}\] | integer | 0, 1, 2, 3, 4 |
|
S_bep
|
\[S_{bep}\] | salinity limitation value at maximum salinity (\(S_{maxsp}\)) | \[\small{-}\] | float | NA |
|
S_maxsp
|
\[S_{maxsp}\] | maximum salinity where growth is possible | \[\small{g/kg}\] | float | NA |
|
S_opt
|
\[S_{opt}\] | optimal salinity for growth | \[\small{g/kg}\] | float | NA |
|
| Nitrogen | ||||||
simDINUptake
|
\[\Theta_{din}^{phy}\] | switch for the selected group to simulate \(DIN\) uptake | \[\small{-}\] | integer | 0, 1 |
|
simDONUptake
|
\[\Theta_{don}^{phy}\] | switch for the selected group to simulate \(DON\) uptake | \[\small{-}\] | integer | 0 |
|
simNFixation
|
\[\Theta_{n2}^{phy}\] | switch for the selected group to simulate \(N_2\) fixation | \[\small{-}\] | integer | 0, 1 |
|
simINDynamics
|
\[\Theta_{in}^{phy}\] | switch for the selected group to simulate dynamic intracellular \(N\) store | \[\small{-}\] | integer | 0, 1, 2 |
|
N_o
|
\[N_o\] | external \(DIN\) concentration below which uptake is 0 | \[\small{mmol\: N/m^3}\] | float | NA |
|
K_N
|
\[K_N\] | half-saturation concentration of nitrogen | \[\small{mmol\: N/m^3}\] | float | NA |
|
X_ncon
|
\[\chi_{ncon}^{PHY}\] | constant internal nitrogen concentration | \[\small{mmol\: N/m^3}\] | float | NA |
used if simINDynamics = 0 or 1
|
X_nmin
|
\[\chi_{nmin}^{PHY}\] | minimum internal nitrogen concentration | \[\small{mmol\: N/m^3}\] | float | NA |
used if simINDynamics = 2
|
X_nmax
|
\[\chi_{nmax}^{PHY}\] | maximum internal nitrogen concentration | \[\small{mmol\: N/m^3}\] | float | NA |
used if simINDynamics = 2
|
R_nuptake
|
\[R_{nuptake}^{PHY}\] | maximum nitrogen uptake rate | \[\small{mmol\: N/m^3/d\: /(mmol\: C/m^3)}\] | float | NA |
used if simINDynamics = 2
|
k_nfix
|
\[k_{nfix}\] | growth rate reduction under maximum nitrogen fixation | \[\small{-}\] | float | NA |
used if simINDynamics \(\gt 0\)
|
R_nfix
|
\[R_{nfix}^{PHY}\] | nitrogen fixation rate | \[\small{/d}\] | float | NA |
used if simINDynamics \(\gt 0\)
|
| Phosphorus | ||||||
simDIPUptake
|
\[\Theta_{dip}^{phy}\] | switch for the selected group to simulate \(DIP\) uptake | \[\small{-}\] | integer | NA |
|
simIPDynamics
|
\[\Theta_{ip}^{phy}\] | switch for the selected group to simulate dynamic intracellular \(P\) store | \[\small{-}\] | integer | NA |
|
P_0
|
\[P_o\] | external \(DIP\) concentration below which uptake is 0 | \[\small{mmol\: P/m^3}\] | float | NA |
|
K_P
|
\[K_P\] | half-saturation concentration of phosphorus | \[\small{mmol\: P/m^3}\] | float | NA |
|
X_pcon
|
\[\chi_{pcon}^{PHY}\] | constant internal phosphorus concentration | \[\small{mmol\: P/m^3}\] | float | NA |
|
X_pmin
|
\[\chi_{pmin}^{PHY}\] | minimum internal phosphorus concentration | \[\small{mmol\: P/m^3}\] | float | NA |
|
X_pmax
|
\[\chi_{pmax}^{PHY}\] | maximum internal phosphorus concentration | \[\small{mmol\: P/m^3}\] | float | NA |
|
R_puptake
|
\[R_{puptake}^{PHY}\] | maximum phosphorus uptake rate | \[\small{mmol\: P/m^3/d\: /(mmol\: C/m^3)}\] | float | NA |
|
| Silica | ||||||
simSiUptake
|
\[\Theta_{si}^{phy}\] | switch for the selected group to simulate \(Si\) uptake | \[\small{-}\] | integer | NA |
|
Si_0
|
\[Si_o\] | external \(SiO2\) concentration below which uptake is 0 | \[\small{mmol\: Si/m^3}\] | float | NA |
|
K_Si
|
\[K_{Si}\] | half-saturation concentration of silica uptake | \[\small{mmol\: Si/m^3}\] | float | NA |
|
X_sicon
|
\[\chi_{sicon}^{PHY}\] | constant internal silica concentration | \[\small{mmol\: Si/m^3}\] | float | NA |
|
| Settling | ||||||
w_p
|
\[\omega_{phy}\] | sedimentation rate | \[\small{m/d}\] | float | -1 - 1 | used if \(\Theta_{set}^{phy}\) is 1 or 2 |
d_phy
|
\[d_{phy}\] | phytoplankton group mean cell diameter | \[\small{m}\] | float | NA | used if \(\Theta_{set}^{phy}\) is 3 |
c1
|
\[c_1\] | rate coefficient for density increase | \[\small{kg/m^3/s}\] | float | NA | used if \(\Theta_{set}^{phy}\) is 3 |
c3
|
\[c_3\] | minimum rate of density decrease with time | \[\small{kg/m^3/s}\] | float | NA | used if \(\Theta_{set}^{phy}\) is 3 |
f1
|
\[f_1\] | fraction of maximum intracellular nitrogen where motility tends down towards nutrients | \[\small{-}\] | float | NA | used if \(\Theta_{set}^{phy}\) is 4 |
f2
|
\[f_2\] | fraction of maximum intracellular nitrogen where motility tends up towards light | \[\small{-}\] | float | NA | used if \(\Theta_{set}^{phy}\) is 4 |
The module level parameters and settings are read in as normal through the aed.nml, summarised in Table 10.4.
| AED name | Symbol | Description | Unit | Type | Typical Range | Comments |
|---|---|---|---|---|---|---|
| Groups | ||||||
num_phy
|
\[N_{a}^{phy}\] | number of phytoplankton groups/species | \[\small{-}\] | integer | 1 - 64 |
|
the_phy
|
\[\mathbb{PHY}\] | set of chosen group ID’s within the database file, where \(a \in \mathbb{PHY}\) | \[\small{-}\] | integer | 1, 2, 3, … |
|
settling
|
\[\Theta_{set}^{phy}\] | option to set the method of settling for \(PHY\) group \(a\) | \[\small{-}\] | integer | 0 - 4 |
|
| Microphytobenthos | ||||||
do_mpb
|
\[\Theta_{mpb}^{phy}\] | option to include \(MPB\) as a simulated benthic variable | \[\small{-}\] | float | 0 , 1, 2 |
|
R_mpbg
|
\[R_{mpb-g}\] | maximum growth rate of \(MPB\) | \[\small{/d}\] | float | 0 - 3 |
|
R_mpbr
|
\[R_{mpb-r}\] | dark respiration rate of \(MPB\) | \[\small{/d}\] | float | 0 - 1 |
|
I_Kmpb
|
\[I_{K_{mpb}}\] | half saturation constant for light limitation of growth | \[\small{W/m^2}\] | float | 0 - 100 |
|
mpb_max
|
\[MPB_{max}\] | maximum biomass density of \(MPB\) | \[\small{mmol\: C/m^2}\] | float | 10000 |
|
resuspension
|
\[\Theta_{resus}^{phy}\] | fraction to set the amount of resuspension for \(PHY\) group \(a\) | \[\small{-}\] | float | 0 , 1 |
|
n_zones
|
\[N_{sz}^{mpb}\] | number of benthic zones where \(MPB\) is active | \[\small{-}\] | integer | 0 - 64 |
|
active_zones
|
\[\mathbb{Z}_{sz}^{mpb}\] | set of benthic zones with \(MPB\) active, where \(sz \in \mathbb{Z}\) | \[\small{-}\] | integer | 1, 2, 3, … |
|
resus_link
|
\[-\] | variable simulating resuspension rate to link to | \[\small{-}\] | string |
NCS_resus
|
|
| Links | ||||||
p_excretion_target_variable
|
\[DOP\] | state variable to add DOP excretion | \[\small{mmol\: P/m^3}\] | string |
OGM_dop
|
|
n_excretion_target_variable
|
\[DON\] | state variable to add DON excretion | \[\small{mmol\: N/m^3}\] | string |
OGM_don
|
|
c_excretion_target_variable
|
\[DOC\] | state variable to add DOC excretion | \[\small{mmol\: C/m^3}\] | string |
OGM_doc
|
|
si_excretion_target_variable
|
\[Si\] | state variable to add Si excretion | \[\small{mmol\: Si/m^3}\] | string |
SIL_rsi
|
|
p_mortality_target_variable
|
\[POP\] | state variable to add POP mortality | \[\small{mmol\: P/m^3}\] | string |
OGM_pop
|
|
n_mortality_target_variable
|
\[PON\] | state variable to add PON mortality | \[\small{mmol\: N/m^3}\] | string |
OGM_pon
|
|
c_mortality_target_variable
|
\[POC\] | state variable to add POC mortality | \[\small{mmol\: C/m^3}\] | string |
OGM_poc
|
|
si_mortality_target_variable
|
\[Si\] | state variable to add Si mortality | \[\small{mmol\: Si/m^3}\] | string |
SIL_rsi
|
|
p1_uptake_target_variable
|
\[FRP\] | state variable to provide FRP for growth | \[\small{mmol\: P/m^3}\] | string |
PHS_frp
|
|
n1_uptake_target_variable
|
\[NO_3\] | state variable to provide \(NO_3\) for growth | \[\small{mmol\: N/m^3}\] | string |
NIT_nit
|
|
n2_uptake_target_variable
|
\[NH_4\] | state variable to provide \(NH_4\) for growth | \[\small{mmol\: N/m^3}\] | string |
NIT_amm
|
|
si_uptake_target_variable
|
\[Si\] | state variable to provide \(Si\) for growth | \[\small{mmol\: Si/m^3}\] | string |
SIL_rsi
|
|
do_uptake_target_variable
|
\[DO\] | state variable to increment \(O_2\) during growth | \[\small{mmol\: O_2/m^3}\] | string |
OXY_oxy
|
|
c_uptake_target_variable
|
\[DIC\] | state variable to provide \(DIC\) during growth | \[\small{mmol\: C/m^3}\] | string |
CAR_dic
|
|
| Advanced | ||||||
dbase
|
\[-\] | phytoplankton parameter database file | \[\small{-}\] | string |
aed_phyto_pars.csv
|
aed_dbase link |
min_rho
|
\[\rho_{min}^{phy}\] | minimum cellular density | \[\small{kg/m^3}\] | float | 900 | used if \(\Theta_{set}^{phy}\) is 3 |
max_rho
|
\[\rho_{max}^{phy}\] | maximum cellular density | \[\small{kg/m^3}\] | float | 1200 | used if \(\Theta_{set}^{phy}\) is 3 |
diag_level
|
\[-\] | extent of diagnostic output | \[\small{-}\] | integer | 0 - 10 | see Table X.X |
10.4 Setup & Configuration
10.4.1 Setup Example
An example aed.nml configuration block for the aed_phytoplankton module that includes a single simulated group plus microphytobenthos (MPB) and resuspension effects, and doesn’t consider Si limitation, is shown below:
&aed_phytoplankton
!-- Configure phytoplankton groups to simulate
num_phytos = 1
the_phytos = 1
settling = 1
!-- Benthic phytoplankton group (microphytobenthos)
do_mpb = 1
R_mpbg = 0.5
R_mpbr = 0.05
I_Kmpb = 100.
mpb_max = 2000.
resuspension = 0.45
n_zones = 4
active_zones = 2,3,4,5
resus_link = 'NCS_resus'
!-- Set link variables to other modules
p_excretion_target_variable ='OGM_dop'
n_excretion_target_variable ='OGM_don'
c_excretion_target_variable ='OGM_doc'
si_excretion_target_variable =''
p_mortality_target_variable ='OGM_pop'
n_mortality_target_variable ='OGM_pon'
c_mortality_target_variable ='OGM_poc'
si_mortality_target_variable =''
p1_uptake_target_variable ='PHS_frp'
n1_uptake_target_variable ='NIT_nit'
n2_uptake_target_variable ='NIT_amm'
si_uptake_target_variable =''
do_uptake_target_variable ='OXY_oxy'
c_uptake_target_variable =''
!-- General options
dbase = '../External/AED/aed_phyto_pars.nml'
diag_level = 1
/Note that when simulating benthic phytoplankton, the bottom zones in the model to be active must be selected.
Another example aed.nml block for the phytoplankton module that includes no benthic (bottom) phytoplankton, and three different groups is shown below:
&aed_phytoplankton
!-- Configure phytoplankton groups to simulate
num_phytos = 3
the_phytos = 1,2,3 ! cyanos,greens,diatoms
settling = 3,1,1 ! approach to settling/migration
!-- Benthic phytoplankton group (microphytobenthos)
do_mpb = 0
!-- Set link variables to other modules
p_excretion_target_variable ='OGM_dop'
n_excretion_target_variable ='OGM_don'
c_excretion_target_variable ='OGM_doc'
si_excretion_target_variable=''
p_mortality_target_variable ='OGM_pop'
n_mortality_target_variable ='OGM_pon'
c_mortality_target_variable ='OGM_poc'
si_mortality_target_variable=''
p1_uptake_target_variable ='PHS_frp'
n1_uptake_target_variable ='NIT_amm'
n2_uptake_target_variable ='NIT_nit'
si_uptake_target_variable ='SIL_rsi'
do_uptake_target_variable ='OXY_oxy'
c_uptake_target_variable ='CAR_dic'
!-- General options
dbase = 'aed/aed_phyto_pars.csv'
diag_level = 10
min_rho = 900.0
max_rho = 1200.0
/The numbers reported here are for example purposes and should be reviewed before use based on the users chosen site context.
In addition to adding the above code block to aed.nml, users must also supply a valid AED phytoplankton parameter database file (aed_phyto_pars).
The database file can be supplied in either NML or CSV format, though after AED 2.0 it is reccomended users use the CSV option.
10.5 Case Studies & Examples
10.5.1 Case Study : Falling Creek Reservoir
Falling Creek Reservoir (FCR) is a water supply reservoir in Virginia.
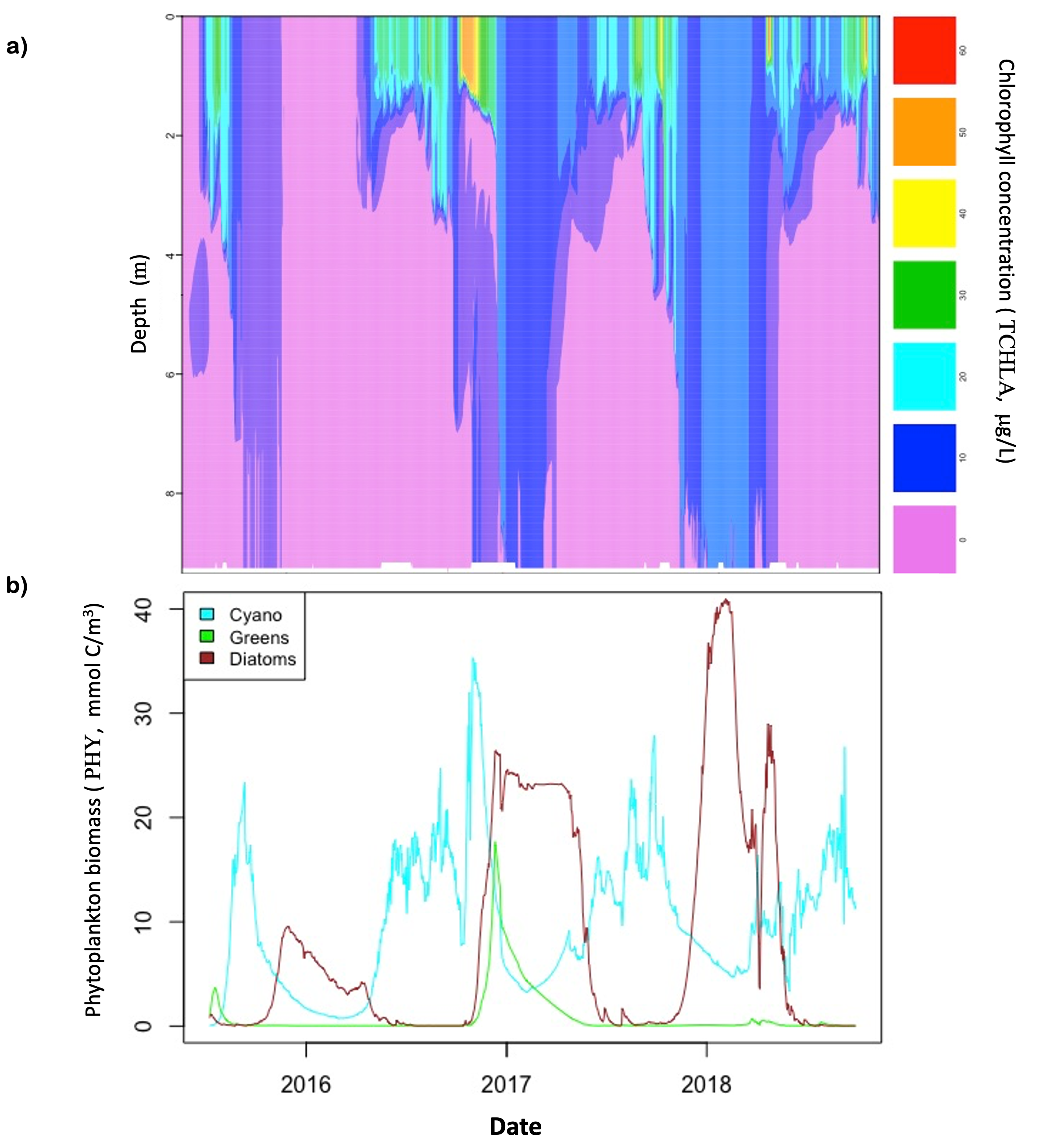
An example GLM-AED simulation for FCR is available in the GLM example simulations provided on GitHub.